사실 인접행렬 방법은 정점 개수가 많아지면 메모리 낭비도 되고 시간 복잡도도 길어지므로, 인접리스트로 푸는 게 좋다.
문제
방향그래프가 주어지면 1번 정점에서 N번 정점으로 가는 모든 경로의 가지 수를 출력하는 프로그램을 작성하세요. (한번 방문한 노드는 다시 방문할 수 없습니다)
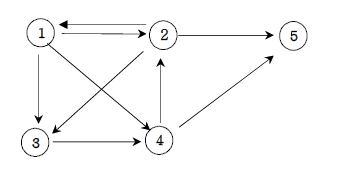
위 그래프에서 1번 정점에서 5번 정점으로 가는 가지 수는
1 2 3 4 5
1 2 5
1 3 4 2 5
1 3 4 5
1 4 2 5
1 4 5
총 6 가지입니다.
▣ 입력설명
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연결정보가 주어진다.
▣ 출력설명
총 가지수를 출력한다.
▣ 입력예제 1
5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5
▣ 출력예제 1
6
풀이
정점의 방향을 이차원 배열을 선언해 인접행렬 방식으로 저장하고, 방문 중복을 막기 위해서 ch 배열로 체크한다.
DFS로 풀면 된다.
코드
import java.util.Scanner;
public class Main {
static int n, m, answer = 0;
static int[][] graph; //인접행렬
static int[] ch; //방문한 적이 있으면 값이 1
public static void DFS(int v) {
if(v == n) {
answer++; //가지수 +1
}
else {
//정점 순회
for(int i=1; i<=n; i++) { //1~n
//갈 수 있는 정점이고, 방문한 적이 없으면 방문
if(graph[v][i] == 1 && ch[i] == 0) {
ch[i] = 1; //방문 체크
DFS(i);
ch[i] = 0; //다시 돌아왔을 때 방문 체크 취소
}
}
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
n = in.nextInt();//정점의 수 1~20
m = in.nextInt(); //간선의 수
graph = new int[n+1][n+1]; //인덱스 번호 = 정점 번호 1~n번
ch = new int[n+1];
for(int i=0; i<m; i++) {
int a = in.nextInt();
int b = in.nextInt();
graph[a][b] = 1;
}
ch[1] = 1; //1부터 시작
DFS(1);
System.out.println(answer);
}
}
'PS(Java) > 인프런 강의 문제' 카테고리의 다른 글
| [PS] 인프런 강의 - Graph 4. 그래프 최단거리(BFS) (0) | 2022.09.26 |
|---|---|
| [PS] 인프런 강의 - Graph 3. 경로 탐색(인접 리스트) (0) | 2022.09.26 |
| [PS] 인프런 강의 - Graph 1. 그래프와 인접행렬 (0) | 2022.09.25 |
| [PS] 인프런 강의 - Tree 5. Tree 말단 노드까지의 가장 짧은 경로 (0) | 2022.09.25 |
| [PS] 인프런 강의 - Tree 4. 송아지 찾기 (BFS) (0) | 2022.09.21 |
![[PS] 인프런 강의 - Graph 2. 경로 탐색(인접 행렬)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FuYq4D%2FbtrMTWSaPsx%2FVr716Li1TwUIqxGHlZMeDK%2Fimg.png)